Blink में सीएसएस कॉर्नर-शेप लागू करने के कॉर्नर केस

Noam Rosenthal

पब्लिश होने की तारीख: 19 फ़रवरी, 2026

Chrome ने 2025 में सीएसएस की एक सुविधा लॉन्च की थी. यह सुविधा corner-shape थी. इसकी मदद से, border-radius वाले कोने का आकार तय किया जा सकता है. इसके लिए, bevel और scoop जैसे कीवर्ड का इस्तेमाल करें. superellipse फ़ंक्शन का इस्तेमाल भी किया जा सकता है. यह फ़ंक्शन, -Infinity और Infinity के बीच की वैल्यू लेता है.

इस सुविधा और इसके काम करने के तरीके के बारे में ज़्यादा जानने के लिए, अमित शीन का Frontend Masters पर मौजूद लेख पढ़ें.

इस सुविधा को 2025 की शुरुआत में लागू करते समय, मुझे कुछ दिलचस्प चुनौतियों का सामना करना पड़ा. ये चुनौतियां अलग-अलग तरह की थीं. मुझे सुपरलिप्स, Blink में बॉर्डर पेंटिंग, और 2D ग्राफ़िक्स के लिए वेक्टर मैथ का इस्तेमाल करने के बारे में बहुत कुछ सीखने को मिला.

इस दस्तावेज़ में, मैंने कुछ ऐसी बातें शेयर की हैं जो मैंने सीखी हैं. ये बातें अन्य लोगों के लिए भी दिलचस्प हो सकती हैं.

उत्तल और अवतल आकृतियों की समरूपता

आम तौर पर, superellipse (k) की वैल्यू 0 और Infinity के बीच होती हैं. इसमें 0 और 1 के बीच की वैल्यू कॉनकेव होती हैं और बाकी वैल्यू कॉन्वेक्स होती हैं. 1, bevel होता है. सीएसएस स्पेसिफ़िकेशन में, superellipse की वैल्यू -Infinity और Infinity के बीच होती हैं. साथ ही, ये 2k को दिखाती हैं. इससे एक सिमिट्री बनती है, क्योंकि कोई भी पॉज़िटिव वैल्यू, उसकी नेगेटिव वैल्यू की मिरर इमेज जैसी दिखती है.

हालांकि, डिफ़ॉल्ट रूप से superellipse फ़ॉर्मूला इस तरह काम नहीं करता.

superellipse फ़ॉर्मूला यह है: xk + yk = 1. उल्टा फ़ॉर्मूला, x1/k + y1/k = 1, विज़ुअल तौर पर सिमेट्रिकल कर्व नहीं बनाता है.

उदाहरण के लिए, 2 के k के साथ:

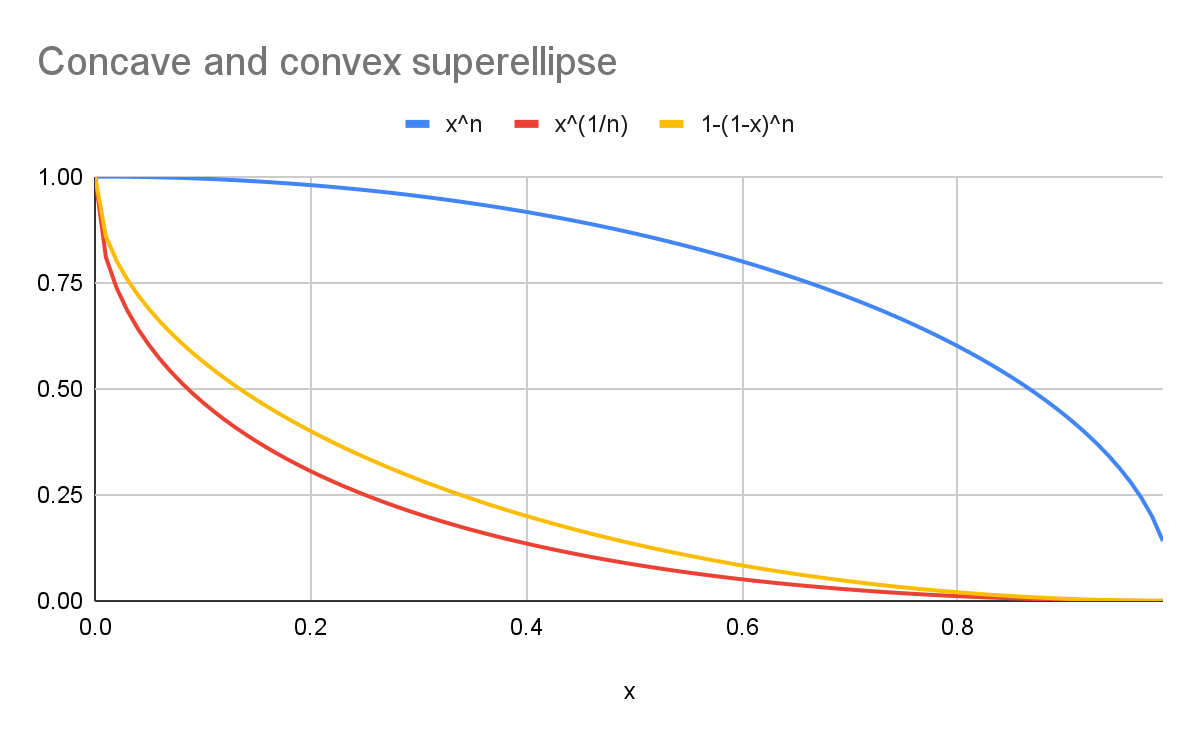
सुपरलिप्स कर्व की तुलना करने वाली इमेज. इसमें गोल सुपरलिप्स (नीला), कैननिकल फ़ॉर्मूला वाला स्कूप सुपरलिप्स (लाल), और विज़ुअल तौर पर सिमेट्रिकल कर्व (पीला) दिखाया गया है.
  • नीला कर्व, राउंड superellipse (y=xn) को दिखाता है.
  • लाल रंग का कर्व, कैननिकल फ़ॉर्मूले (y=x1/n) के साथ scoop superellipse को दिखाता है.
  • पीला कर्व, नीले कर्व (y=1-(1-x)n) के हिसाब से विज़ुअल तौर पर सिमेट्रिकल कर्व को दिखाता है.

चार्ट में दिखाया गया है कि दोनों आकृतियां एक जैसी नहीं हैं!

हम इसके गणित के बारे में ज़्यादा जानकारी नहीं देंगे, लेकिन यह दोहरे नियमों और घुमाव को देखने के हमारे तरीके से जुड़ा है.

स्पेसिफ़िकेशन और लागू करने के मामले में, हम यहां कुछ विज़ुअल दिखा रहे हैं. इसलिए, कॉनकेव शेप का हिसाब लगाते समय, हम सिमेट्रिकल इक्विवेलेंट का इस्तेमाल करते हैं. बाकी गणित, कॉन्वेक्स शेप (k>=1 या पॉज़िटिव सुपरलिप्स वैल्यू) पर की जाती है.

बंद फ़ॉर्मूला

अगली चुनौती, superellipse के कर्व या परिधि को क्लोज़्ड फ़ॉर्म में दिखाना है. यह अंकगणित की सामान्य संक्रियाओं से बना एक फ़ॉर्मूला है. यह परफ़ॉर्मेंस के लिए ज़रूरी है. इससे सिस्टम, superellipse रेंडरिंग को ग्राफ़िक्स इंजन को सौंप देता है.

Skia जैसे ग्राफ़िक्स इंजन, बेज़ियर कर्व के बारे में जानते हैं. इसलिए, superellipse को कुछ बेज़ियर कर्व के साथ दिखाने से, superellipse कर्व को रेंडर करने में आसानी होती है. ये बेज़ियर कर्व, superellipse के पेरीमीटर के आस-पास होते हैं.

अच्छी बात यह है कि सिंबॉलिक रिग्रेशन का इस्तेमाल करके, हम एक ऐसा फ़ॉर्मूला ढूंढ सकते हैं जो कॉन्वेक्स कॉर्नर के आधे हिस्से को एक सिंगल क्यूबिक बेज़ियर कर्व के तौर पर दिखाता है.

क्यूबिक बेज़ियर कर्व में चार पॉइंट होते हैं:

  • पहला पॉइंट (0, 1) है.
  • आखिरी पॉइंट, असल सुपरलिप्स का आधा कोना होता है: 0.51/k,0.51/k.
  • पहला कंट्रोल पॉइंट, शुरुआती पॉइंट के लेवल पर ही अंदर की ओर बढ़ता है: (a, 1).
  • दूसरा कंट्रोल पॉइंट, आधे कोने पर मौजूद होता है: (0.51/k - b,0.51/k + b).

यहां इस्तेमाल की गई हाफ़-कॉर्नर वैल्यू, एक बहुत ही ज़रूरी कोऑर्डिनेट है. इसका इस्तेमाल हम आगे चलकर अन्य हिसाब-किताब के लिए करेंगे.

यहां a और b को सिंबॉलिक रिग्रेशन का इस्तेमाल करके k से कंप्यूट किया जाता है.

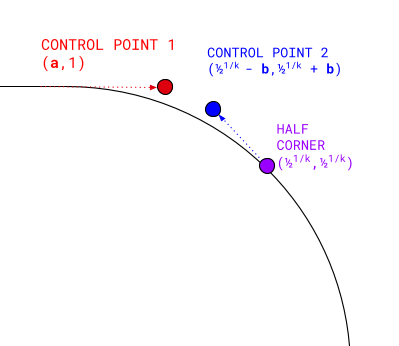
कर्व पर मैप किए गए कंट्रोल पॉइंट का इलस्ट्रेशन.
डेमो के लिए, यह Codepen देखें.

इन चार पॉइंट की गिनती करने और इनके बीच एक क्यूबिक बेज़ियर कर्व रेंडर करने से, दिए गए k के साथ एक क्लोज़्ड फ़ॉर्म कॉन्वेक्स हाफ़ कॉर्नर मिलता है. इसके बाद, हम नतीजों को घुमाकर कोने के बाकी हिस्से को भर सकते हैं. साथ ही, उन्हें अन्य कोनों पर लागू कर सकते हैं और उन्हें फ़्लिप करके, अवतल आकार में रेंडर कर सकते हैं.

गणित के ज़्यादा जटिल फ़ॉर्मूले में न जाते हुए, a और b को कैलकुलेट करने का फ़ॉर्मूला यह है:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

बॉर्डर और शैडो

सिस्टम, कोने की परिधि के पाथ का हिसाब लगाने के साथ-साथ यह भी हिसाब लगाता है कि अंदर की ओर ऑफ़सेट होने पर यह कैसा दिखता है (बॉर्डर या इंसर्ट box-shadow) या बाहर की ओर ऑफ़सेट होने पर यह कैसा दिखता है (outline या सामान्य box-shadow). सामान्य ग्राफ़िक्स लाइब्रेरी में, यह काम स्ट्रोकिंग की मदद से किया जाता है.

हालांकि, सीएसएस में बॉर्डर और शैडो की रेंडरिंग की विशेषताएं, स्ट्रोकिंग से अलग होती हैं:

  • बॉर्डर एक जैसे नहीं हैं.
  • उदाहरण के लिए, ऊपरी बॉर्डर 10 पिक्सल और दायां बॉर्डर 5 पिक्सल का हो सकता है. साथ ही, कॉर्नर इन दोनों के बीच इंटरपोलेट करता है.
  • इसके अलावा, ये दोनों तरफ़ न जाकर अंदर की ओर जाते हैं.
  • परछाइयां और आउटलाइन, स्ट्रोक की तरह रेंडर नहीं होती हैं.
  • इसके बजाय, ये इस तरह से एडजस्ट होते हैं कि कोने शार्प दिखें.

आम तौर पर, बॉर्डर और शैडो रेंडर करने का तरीका, corner-shape वैल्यू के लिए अच्छी तरह से काम करता है. ये वैल्यू, गोल या इससे ज़्यादा कॉन्वेक्स (उभरी हुई) होती हैं. उदाहरण के लिए, squircle. साथ ही, इसे 90 डिग्री घुमाया जा सकता है. ऐसा उन शेप के लिए किया जाता है जो scoop से ज़्यादा कॉनकेव (धंसी हुई) होती हैं. हालांकि, यह डिफ़ॉल्ट तरीका, -1 और 1 के बीच की corner-shape वैल्यू के लिए काम नहीं करता. ऐसा इसलिए, क्योंकि बॉर्डर या शैडो को किनारे के समानांतर ऑफ़सेट करने से एक ऐसा कोना बनता है जिसकी चौड़ाई एक जैसी नहीं होती.

उदाहरण के लिए, bevel कोने को लेकर, बॉर्डर को दोनों ओर से कुछ पिक्सल तक ऑफ़सेट करने पर "बेली" इफ़ेक्ट बनता है. इसमें कोने का बीच वाला हिस्सा, किनारों से ज़्यादा चौड़ा दिखता है.

इसके लिए, हमारा लक्ष्य ऐसा इफ़ेक्ट बनाना है जो स्ट्रोक की तरह काम करे. इसके लिए, कोने की कर्व की शुरुआत में सामान्य ढूंढें और इसे border या shadow-spread की चौड़ाई जितना लंबा बनाएं.

हालांकि, ऐसा सिर्फ़ सब-एलिप्स (bevel और राउंड के बीच) के लिए ज़रूरी है. हाइपर-एलिप्स, जैसे कि squircle उम्मीद के मुताबिक काम करते हैं.

सब-एलिप्स कर्व का नॉर्मल पता करने के लिए, इसके क्वाड्रेटिक कर्व का नॉर्मल पता करना काफ़ी है. ऐसा इसलिए, क्योंकि सब-एलिप्स और उनके क्वाड्रेटिक कर्व एक-दूसरे के काफ़ी करीब होते हैं.

पहले से कंप्यूट किए गए उसी हाफ़-कॉर्नर का इस्तेमाल करके, एक ऐसी क्वाडैटिक कर्व का पता लगाया जा सकता है जिसका मिडिल पॉइंट एक जैसा हो. इसके बाद, क्वाडैटिक कंट्रोल पॉइंट निकाला जा सकता है. इसके बाद, नॉर्मल कंप्यूट करना आसान हो जाता है.

सामान्य, border-width या shadow-spread के बराबर लंबाई के साथ जारी रहता है. इसके बाद, यह नतीजे में मिली कर्व को किनारों (बॉर्डर के लिए अंदरूनी किनारा, शैडो के लिए बाहरी किनारा) से काटता है, ताकि एक लगातार पाथ बनाया जा सके.

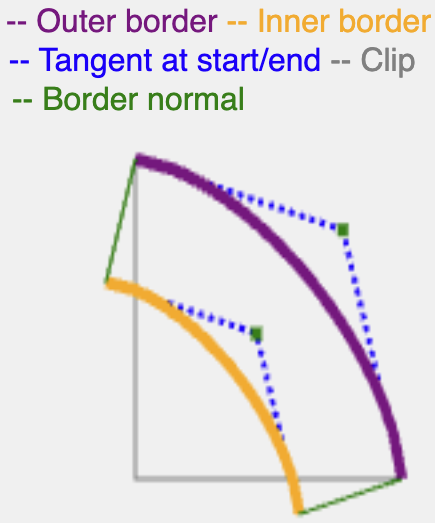
बॉर्डर वाले कोने की इमेज. इसमें दिखाया गया है कि बॉर्डर की शेप तय करने के लिए, सामान्य को कैसे बढ़ाया जाता है.
CodePen पर यह उदाहरण देखें.

superellipse के लिए स्पर्शरेखा का हिसाब लगाने के ज़्यादा सटीक तरीके मौजूद हैं. हालांकि, यह तरीका असरदार है और इससे बॉर्डर और शैडो रेंडर करने के लिए सही नतीजे मिलते हैं.

कलर जॉइन

ब्राउज़र में पेंटिंग का एक दिलचस्प हिस्सा होता है, जिसे सीएसएस में तय नहीं किया गया है. यह ऐसे बॉर्डर रेंडर करता है जिनमें एक जैसे रंग या स्टाइल नहीं होते. उदाहरण के लिए, जहां आपके एलिमेंट में हरे रंग का सॉलिड टॉप बॉर्डर और पीले रंग का डॉटेड राइट बॉर्डर है. इन मामलों में, मिटर एक कट लाइन होती है. यह बॉर्डर के किनारे के कोने और पैडिंग के किनारे के कोने के बीच से जाती है. यह आस-पास के किनारों के बीच बॉर्डर बनाता है.हालांकि, इसे तय नहीं किया गया है, लेकिन रेंडरिंग ब्राउज़र के हिसाब से कुछ हद तक एक जैसी होती है.

इसे Blink और अन्य ब्राउज़र में इस तरह लागू किया जाता है. पेंट की जाने वाली एज को इस तरह से काटा जाता है कि वह मिटर पर क्रॉस करने वाले पॉलीगॉन की तरह दिखे. इसे इस तरह से कैलकुलेट किया जाता है कि इसमें काम की एज शामिल हो, लेकिन अन्य एज शामिल न हों. इससे ब्लिडिंग से बचा जा सकता है. साथ ही, किसी एक किनारे को गलत स्टाइल और रंग से पेंट करने से भी बचा जा सकता है.

अब तक इस पॉलीगॉन की गणना करना काफ़ी आसान था, क्योंकि सामान्य गोल कोनों की वजह से कोने वाले हिस्से कभी ओवरलैप नहीं हो सकते. हालांकि, हाइपो-एलिप्स और खास तौर पर कॉनकेव सुपरएलिप्स (नेगेटिव superellipse वैल्यू) के साथ यह बदल जाता है. इनसे काफ़ी दिलचस्प आकार बनाए जा सकते हैं. हालांकि, इससे इंटरसेक्शन पॉलीगॉन में ओवरलैप होने और "ब्लिडिंग" की समस्या होने की काफ़ी आशंका रहती है.

यहां दी गई सीएसएस देखें:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}
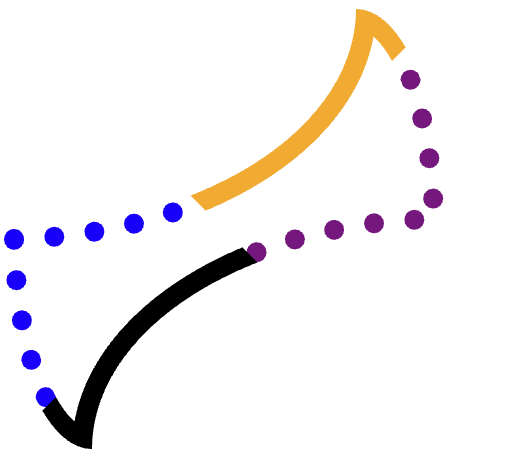
सीएसएस एलिमेंट का उदाहरण, जिसमें एक जैसी बॉर्डर नहीं हैं. इसमें नारंगी, बैंगनी रंग के डॉट वाली, काली, और नीले रंग के डॉट वाली बॉर्डर दिखाई गई हैं.

हमें हर किनारे (नारंगी, बैंगनी रंग के डॉट वाला, काला, नीले रंग के डॉट वाला) को अलग-अलग काटना है. इसके बाद, पाथ बनाना है.

इसके लिए, आपको इमेज को इस तरह से काटना होगा कि वह अन्य तीन कोनों में से किसी भी कोने पर ओवरलैप न करे.

उदाहरण के लिए, नारंगी रंग (सबसे ऊपर) वाला किनारा देखें.

ऐसा सटीक पॉलीगॉन ढूंढना मुश्किल है जिसमें पूरा किनारा शामिल हो और वह बैंगनी, पीले या काले किनारों में न दिखे. कुछ अन्य शेप बनाना ज़्यादा मुश्किल होता है.

इस प्रोसेस में तीन क्लिप शामिल हैं.

पहली क्लिप में पूरा किनारा और पूरा कोना (बिना मिटर के) शामिल है. उदाहरण के लिए:

यह क्लिप किए गए कोने वाली शेप है. इसमें दो कोने दिखाए गए हैं. एक स्कूप और एक गोल.

इसमें दो कोने (एक scoop, एक गोल) होते हैं. इनके बीच में बहुत कम किनारा होता है और ये सिरों पर जुड़े होते हैं.

इस शेप से, दूसरी ओर के किनारे के साथ ओवरलैप खत्म हो जाता है. अब सिर्फ़ दो मिटर का ध्यान रखना होता है.

इसके लिए, इस कोने से एक ऐसा पॉलीगॉन काटा जाता है जो बॉर्डर-एज और पैडिंग-एज के कोनों के बीच से गुज़रता है. यह तब रुकता है, जब यह एज से टकराने वाला होता है:

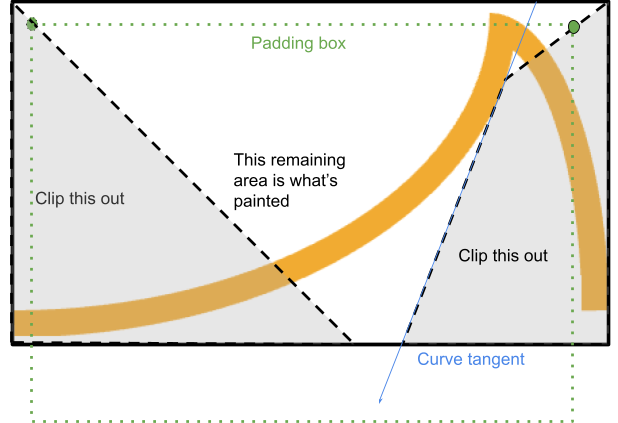
क्लिप किए जाने वाले हिस्सों का डेमो.

सिस्टम उस पॉइंट का पता लगाता है जहां बॉर्डर एज से पैडिंग एज तक की लाइन, कर्व के टैंजेंट से मिलती है. यह टैंजेंट, कर्व के शुरुआती पॉइंट से होता है. ऐसा तब होता है, जब कर्व कॉनकेव होता है.

अगर वह पॉइंट रेंडर किए गए एरिया के अंदर है, तो प्रोसेस वहीं रुक जाती है. इसके बाद, वह उस स्पर्शरेखा के साथ तब तक आगे बढ़ती है, जब तक कि वह बॉर्डर बॉक्स से फिर से न मिल जाए. इससे एक क्वाड पूरा हो जाता है.

इसके अलावा, एक सामान्य त्रिकोण को क्लिप किया जा सकता है.

खास जानकारी

वेब प्लैटफ़ॉर्म, वेब डिज़ाइनर और डेवलपर को कई तरह की सुविधाएं उपलब्ध कराता है. कभी-कभी, एक न्यूमेरिक वैल्यू लेने वाली सीएसएस प्रॉपर्टी, रेंडरिंग को सटीक और एक जैसा बनाने के लिए, बैकग्राउंड में काफ़ी जटिलता को छिपा देती है.

corner-shape सुविधा में काफ़ी जटिलता थी. इस दस्तावेज़ का मकसद, आने वाले समय में इस सुविधा पर काम करने वाले डेवलपर की मदद करना है. ये डेवलपर, Blink, अन्य ब्राउज़र या स्पेसिफ़िकेशन पर काम करते हैं.