Opublikowano: 19 lutego 2026 r.
Jedną z funkcji CSS, które Chrome wprowadził w 2025 r., była corner-shape.
Pozwala to określić kształt rogu, który ma border-radius, za pomocą słów kluczowych takich jak bevel i scoop. Możesz też użyć funkcji superellipse, która przyjmuje wartość z zakresu od -Infinity do Infinity.
Szczegółowy opis tej funkcji i jej działania znajdziesz w obszernym artykule Amita Sheena na stronie Frontend Masters.
Podczas wdrażania tej funkcji na początku 2025 roku napotkałem kilka ciekawych wyzwań o różnym stopniu złożoności. Wiele się nauczyłem o superelipsach, malowaniu obramowań w Blinku i wykorzystaniu matematyki wektorowej w grafice 2D.
W tym dokumencie dzielę się niektórymi z tych informacji, które mogą być interesujące również dla innych osób.
Symetria kształtów wypukłych i wklęsłych
Wartości superellipse (k) zwykle mieszczą się w zakresie od 0 do Infinity, przy czym wartości od 0 do 1 są wklęsłe, a pozostałe wypukłe (1 to bevel). W specyfikacji CSS wartości superellipse mieszczą się w zakresie od -Infinity do Infinity i reprezentują 2k. Dzięki temu powstaje symetria, ponieważ każda wartość dodatnia wygląda jak odbicie lustrzane jej odpowiednika ujemnego.
Domyślnie jednak formuła superellipse nie działa w ten sposób.
Wzór na superellipse to: xk + yk = 1. Formuła odwrotna, x1/k + y1/k = 1, nie daje wizualnie symetrycznej krzywej.
Na przykład w przypadku wartości k równej 2:
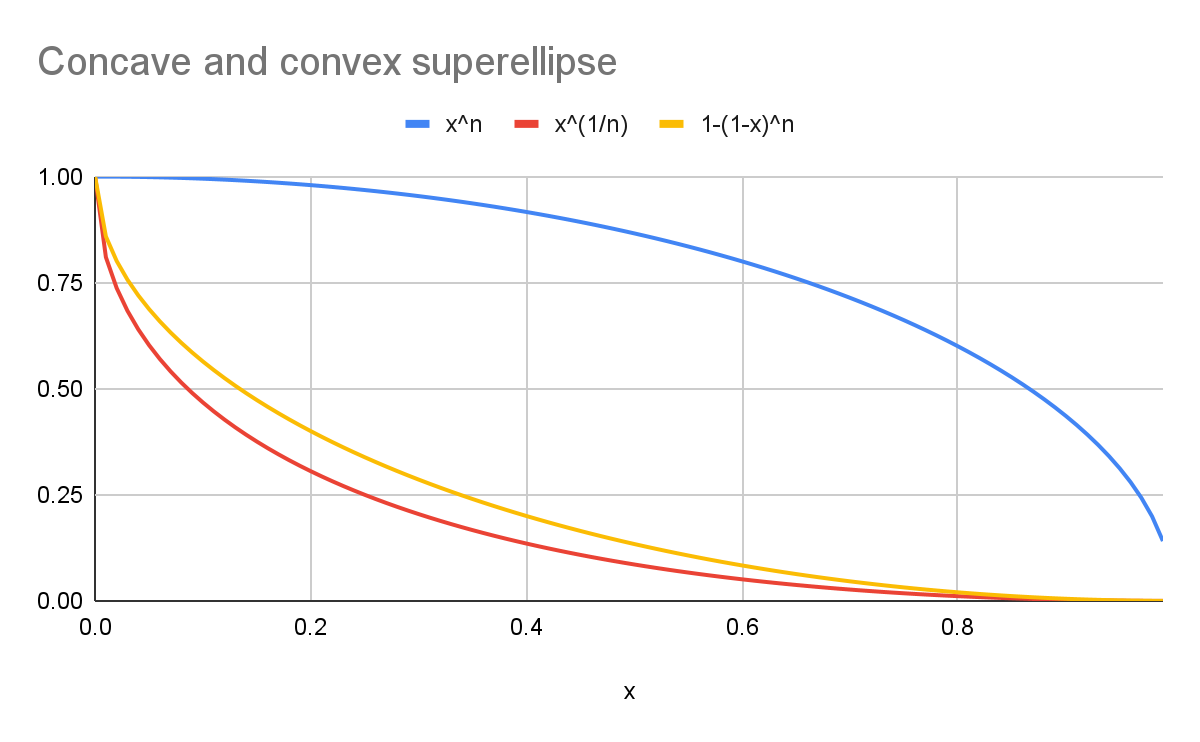
- Niebieska krzywa przedstawia okrąg
superellipse(y=xn). - Czerwona krzywa przedstawia
scoopsuperellipsez kanonicznym wzorem (y=x1/n). - Żółta krzywa jest wizualnie symetryczna względem niebieskiej krzywej (
y=1-(1-x)n).
Jak widać na wykresie, kształty nie są takie same.
Nie będę się zagłębiać w matematykę, ale ma to związek z podwójnymi normami i tym, jak postrzegamy krzywiznę.
W przypadku specyfikacji i implementacji reprezentujemy tutaj coś wizualnego, więc podczas obliczania kształtów wklęsłych używamy odpowiedników symetrycznych. Pozostałe obliczenia są wykonywane na kształtach wypukłych (k>=1 lub dodatnich wartościach superelipsy).
Formuła w postaci zamkniętej
Kolejnym wyzwaniem jest przedstawienie krzywej, czyli obwodu superellipse, w postaci zamkniętej, czyli za pomocą wzoru składającego się z prostych działań arytmetycznych.
Jest to niezbędne dla wydajności, ponieważ umożliwia przekazanie renderowania do silnika graficznego.superellipse
Silniki graficzne, takie jak Skia, znają krzywe Beziera, więc przedstawienie znaku superellipse za pomocą niewielkiej liczby krzywych Beziera, które przybliżają jego obwód, zwiększa wydajność renderowania krzywej superellipse.
Na szczęście za pomocą regresji symbolicznej możemy znaleźć formułę, która przedstawia połowę wypukłego rogu jako pojedynczą krzywą Beziera trzeciego stopnia.
Krzywa Beziera trzeciego stopnia ma 4 punkty:
- Pierwszy punkt to (
0, 1). - Ostatni punkt to rzeczywisty półróg superelipsy:
0.51/k,0.51/k. - Pierwszy punkt kontrolny rozciąga się na tym samym poziomie co punkt początkowy: (
a, 1). - Drugi punkt kontrolny znajduje się po przekątnej połowy rogu:
(0.51/k - b,0.51/k + b).
Użyta tutaj wartość półrogu jest bardzo ważnym współrzędnym, którego będziemy używać w dalszych obliczeniach.
Gdzie a i b są obliczane na podstawie k za pomocą regresji symbolicznej.
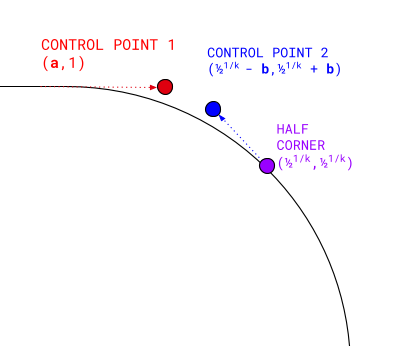
Obliczenie tych 4 punktów i wyrenderowanie między nimi krzywej Béziera trzeciego stopnia daje zamknięty, wypukły półróg o danym k. Następnie możemy obrócić wyniki, aby wypełnić pozostałą część rogu, zastosować je do innych rogów i odwrócić, aby uzyskać odpowiedniki wklęsłe.
Nie zagłębiając się w matematyczne szczegóły, formuła obliczania wartości a i b wygląda tak:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Obramowanie i cienie
Oprócz obliczania ścieżki obwodu rogu system oblicza też, jak wygląda ona po przesunięciu do wewnątrz (obramowanie lub wstawka box-shadow) lub na zewnątrz (outline lub normalny box-shadow). W konwencjonalnych bibliotekach graficznych odbywa się to przez obrysowanie.
Obramowania i cienie w CSS mają jednak charakterystykę renderowania, która różni się od obrysowywania:
- Ramki nie są jednolite.
- Na przykład górna krawędź może mieć 10 pikseli, a prawa – 5 pikseli, a narożnik będzie interpolowany między nimi.
- Poza tym są one skierowane do wewnątrz, a nie na obie strony.
- Cienie i kontury nie są renderowane dokładnie tak samo jak obrys.
- Zamiast tego dostosowują się tak, aby narożniki były ostre.
Zwykła ścieżka renderowania obramowania i cienia sprawdzała się w przypadku wartości corner-shape, które są okrągłe lub bardziej wypukłe (np. squircle), i można ją było obracać o 90 stopni w przypadku kształtów bardziej wklęsłych niż scoop, ale ta domyślna ścieżka nie działa w przypadku wartości corner-shape z zakresu od -1 do 1, ponieważ przesunięcie obramowania lub cienia równolegle do krawędzi powoduje powstanie rogu, który wydaje się mieć nierówną szerokość.
Na przykład wzięcie bevel rogu i przesunięcie krawędzi o kilka pikseli w obie strony tworzy efekt „brzuszka”, w którym środek rogu wygląda na szerszy niż boki.
Aby to uwzględnić, chcemy uzyskać efekt podobny do obrysu – znaleźć wektor normalny krzywej narożnika na początku i ustawić jego długość na szerokość znaku border lub shadow-spread.
Na szczęście jest to konieczne tylko w przypadku podelips (między bevel a okrągłym), ponieważ hiperelipsy, takie jak squircle, działają zgodnie z oczekiwaniami.
Aby znaleźć wektor normalny do krzywej sub-elipsy, wystarczy znaleźć wektor normalny do jej odpowiednika w postaci krzywej kwadratowej, ponieważ sub-elipsy i ich odpowiedniki w postaci krzywych kwadratowych są do siebie zbliżone.
Korzystając z obliczonego wcześniej półrogu, możesz znaleźć krzywą kwadratową, która ma ten sam punkt środkowy, wyprowadzić jej kwadratowy punkt kontrolny, a następnie łatwo obliczyć wektor normalny.
Normalna kontynuacja ma taką samą długość jak border-width lub shadow-spread, a następnie przycina wynikową krzywą do krawędzi (wewnętrznej w przypadku obramowania, zewnętrznej w przypadku cienia), aby utworzyć ciągłą ścieżkę.
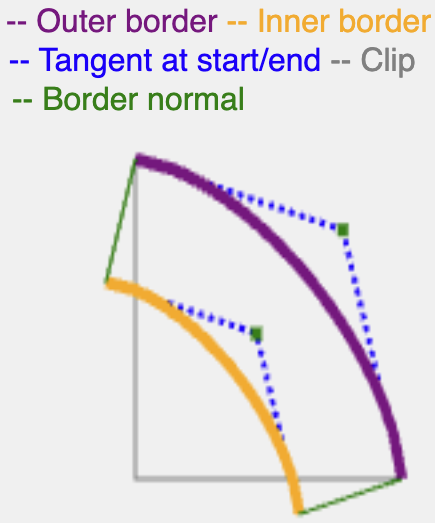
Istnieją bardziej precyzyjne matematycznie sposoby obliczania stycznej do superellipse, ale ta metoda jest wydajna i daje odpowiednie wyniki w przypadku renderowania obramowań i cieni.
Połączenia kolorów
Ciekawy aspekt renderowania w przeglądarkach nie jest określony w CSS. Renderuje obramowania o nierównomiernych kolorach lub stylach. Na przykład element ma zieloną, ciągłą górną krawędź i żółtą, przerywaną prawą krawędź. W takich przypadkach ukośne cięcie to linia cięcia między odpowiednim rogiem krawędzi obramowania a odpowiednim rogiem krawędzi dopełnienia. Tworzy granicę między sąsiednimi krawędziami.Chociaż nie jest to określone, renderowanie jest w pewnym stopniu spójne w różnych przeglądarkach.
W Blinku (i innych przeglądarkach) jest to zaimplementowane w ten sposób: Krawędź, która ma zostać narysowana, jest przycinana w przybliżeniu jak wielokąt przecinający się w miejscu złączenia, w taki sposób, aby obejmowała odpowiednią krawędź, ale nie inne krawędzie. Pozwoli to uniknąć rozlewania się, czyli pomalowania jednego z pozostałych brzegów niewłaściwym stylem i kolorem.
Ten wielokąt był dotychczas stosunkowo prosty do obliczenia, ponieważ w przypadku regularnych zaokrąglonych rogów obszary narożne nigdy nie mogą się nakładać. Zmienia się to jednak w przypadku hipoelips, a zwłaszcza w przypadku wklęsłych superelips (ujemne wartości superellipse). Mogą one tworzyć dość ciekawe kształty, które sprawiają, że proste wielokąty przecięcia są bardzo podatne na nakładanie się i „rozmywanie”.
Rozważmy ten kod CSS:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
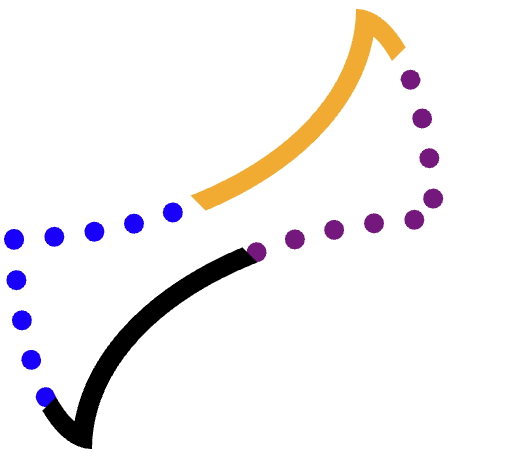
Chcemy przyciąć każdą krawędź (pomarańczową, fioletową z kropkami, czarną, niebieską z kropkami) osobno, a następnie narysować ścieżkę.
Aby to osiągnąć bez nakładania się na pozostałe 3 rogi, konieczne jest staranne przycięcie.
Weźmy na przykład pomarańczową (górną) krawędź.
Trudno jest znaleźć dokładny wielokąt, który obejmuje całą krawędź i nie zachodzi na fioletowe, żółte ani nawet czarne krawędzie. Niektóre inne kształty są trudniejsze.
Ten proces obejmuje 3 klipy.
Pierwszy klip obejmuje całą krawędź z pełnym rogiem (bez ukosu). Na przykład:

Składa się z 2 rogów (1 scoop i 1 okrągły) połączonych na końcach, między którymi jest minimalna krawędź.
Zaczynając od tego kształtu, eliminujemy nakładanie się z przeciwległą krawędzią, a teraz problemem pozostają tylko 2 ukośne połączenia.
Można to osiągnąć, wycinając z tego rogu wielokąt, który przechodzi między narożnikami krawędzi obramowania i krawędzi dopełnienia i zatrzymuje się w momencie, gdy ma się przeciąć z krawędzią:
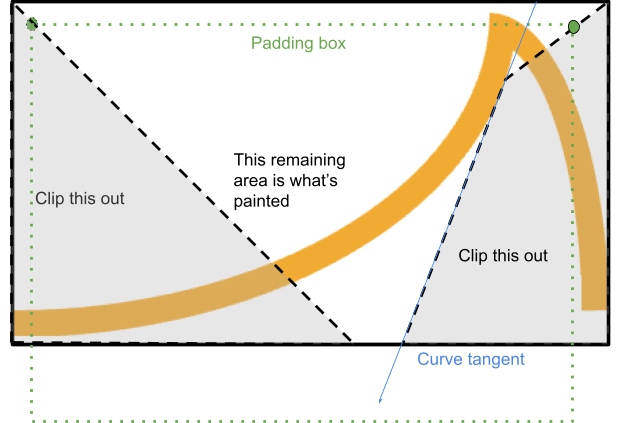
System znajduje punkt, w którym linia od krawędzi obramowania do krawędzi dopełnienia przecina styczną krzywej z odpowiedniego punktu początkowego (jeśli krzywa jest wklęsła).
Jeśli ten punkt znajduje się w obszarze renderowania, proces zatrzymuje się w tym miejscu i jest kontynuowany wzdłuż stycznej, aż ponownie spotka się z ramką, tworząc czworokąt.
W przeciwnym razie można przyciąć prosty trójkąt.
Podsumowanie
Platforma internetowa zapewnia projektantom i programistom stron internetowych duże możliwości. Czasami właściwość CSS, która przyjmuje pojedynczą wartość liczbową, skrywa pod maską znaczną złożoność, aby zapewnić dokładne i spójne renderowanie.
Funkcja corner-shape okazała się zaskakująco złożona. Ta dokumentacja ma pomóc przyszłym programistom pracującym nad tą funkcją w Blinku, innych przeglądarkach lub specyfikacji.

