Fecha de publicación: 19 de febrero de 2026
Una de las funciones de CSS que Chrome lanzó en 2025 fue corner-shape.
Esto te permite definir la forma de una esquina que tiene un border-radius con palabras clave como bevel y scoop. También puedes usar una función superellipse que recibe un valor entre -Infinity y Infinity.
Consulta el extenso artículo de Amit Sheen en Frontend Masters para obtener una excelente descripción general de la función y cómo funciona.
Cuando implementé esta función a principios de 2025, me encontré con algunos desafíos interesantes de diferente complejidad. Aprendí mucho sobre superelipses, pintura de bordes en Blink y el uso de matemáticas vectoriales para gráficos en 2D.
En este documento, comparto algunas de las cosas que aprendí, que también podrían ser interesantes para otras personas.
Simetría de formas convexas y cóncavas
Si bien los valores de superellipse (k) tradicionalmente se encuentran entre 0 y Infinity, en los que los valores entre 0 y 1 son cóncavos y el resto son convexos (1 es bevel), los valores de superellipse en la especificación de CSS se encuentran entre -Infinity y Infinity, y representan 2k. Esto crea una simetría, ya que cualquier valor positivo se ve como la imagen especular de su contraparte negativa.
Sin embargo, de forma predeterminada, la fórmula superellipse no funciona de esa manera.
La fórmula de superellipse es xk + yk = 1. La fórmula inversa, x1/k + y1/k = 1, no produce una curva visualmente simétrica.
Por ejemplo, con un k de 2:
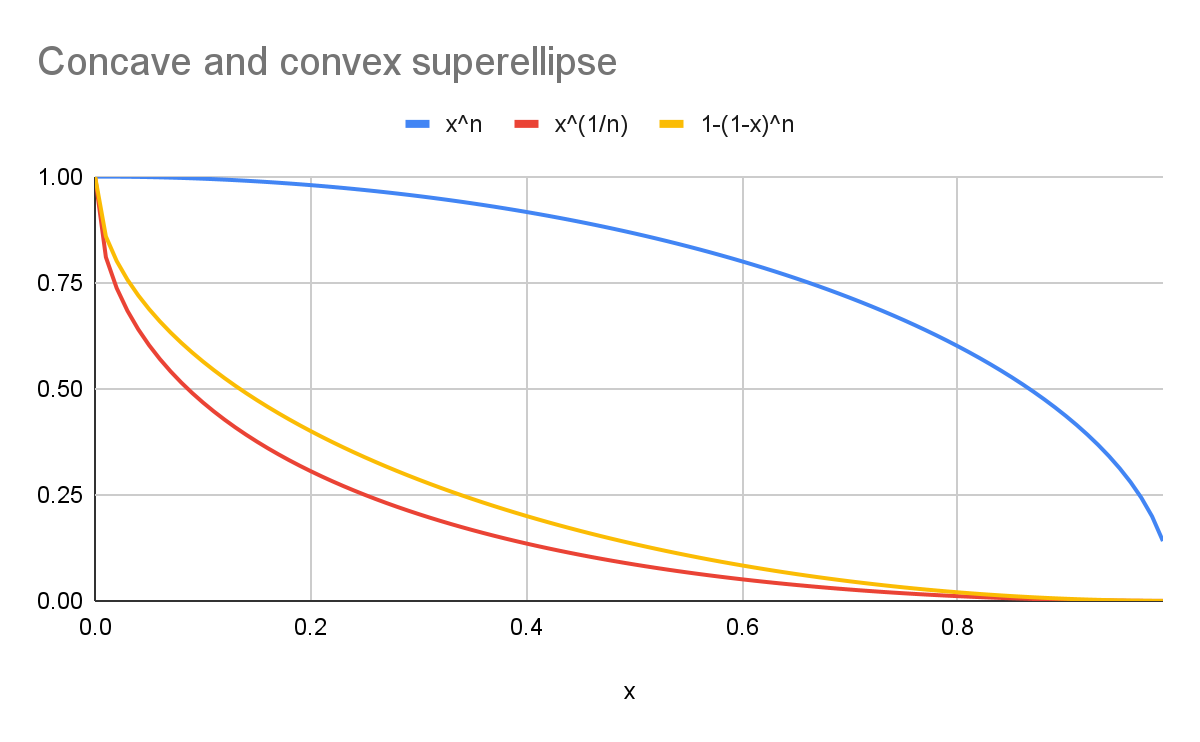
- La curva azul representa una ronda
superellipse(y=xn). - La curva roja representa un
scoopsuperellipsecon la fórmula canónica (y=x1/n). - La curva amarilla representa una curva que es visualmente simétrica a la curva azul (
y=1-(1-x)n).
Como se muestra en el gráfico, las formas no son iguales.
No profundizaré en las matemáticas, pero tiene que ver con las normas duales y cómo percibimos la curvatura.
En términos de especificación e implementación, aquí representamos algo visual, por lo que usamos los equivalentes simétricos cuando calculamos formas cóncavas. El resto de los cálculos se realizan en formas convexas (k>=1 o valores positivos de superelipse).
Fórmula de forma cerrada
El siguiente desafío es representar la curva, o el perímetro del superellipse, en forma cerrada, una fórmula compuesta por operaciones aritméticas simples.
Esto es fundamental para el rendimiento, ya que permite que el sistema entregue la renderización de superellipse al motor de gráficos.
Los motores gráficos, como Skia, conocen las curvas de Bézier, por lo que representar un superellipse con una pequeña cantidad de curvas de Bézier que aproximan su perímetro hace que la renderización de una curva de superellipse sea más eficiente.
Afortunadamente, con la regresión simbólica, podemos encontrar una fórmula que represente la mitad de una esquina convexa como una sola curva de Bézier cúbica.
Una curva de Bézier cúbica tiene cuatro puntos:
- El primer punto es (
0, 1). - El último punto es la mitad de la esquina de la superelipse real:
0.51/k,0.51/k. - El primer punto de control se extiende hacia adentro al mismo nivel que el punto de partida: (
a, 1). - El segundo punto de control es diagonal a la mitad de la esquina:
(0.51/k - b,0.51/k + b).
El valor de media esquina que se usa aquí resulta ser una coordenada muy importante que usaremos para otros cálculos más adelante.
Aquí, a y b se calculan a partir de k con regresión simbólica.
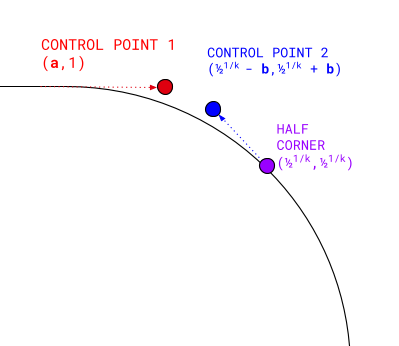
Calcular estos cuatro puntos y renderizar una curva de Bézier cúbica entre ellos proporciona una esquina convexa de forma cerrada con un k determinado. Luego, podemos rotar los resultados para completar el resto de la esquina, aplicarlos a otras esquinas y voltearlos para renderizar los equivalentes cóncavos.
Sin profundizar en los detalles matemáticos, la fórmula para calcular a y b es la siguiente:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Bordes y sombras
Además de calcular la ruta del perímetro de la esquina, el sistema también calcula cómo se ve cuando se desplaza hacia adentro (un borde o una inserción box-shadow) o hacia afuera (un outline o un box-shadow normal). En las bibliotecas de gráficos convencionales, esto se hace con un trazo.
Sin embargo, los bordes y las sombras en CSS tienen características de renderización que difieren del trazo:
- Los bordes no son uniformes.
- Por ejemplo, el borde superior puede ser de 10 píxeles y el borde derecho de 5 píxeles, con la esquina interpolando entre ellos.
- Además, se dirigen hacia adentro en lugar de hacia ambos lados.
- Las sombras y los contornos no se renderizan exactamente como un trazo.
- En cambio, se ajustan para que las esquinas se vean definidas.
Si bien la ruta de renderización habitual de bordes y sombras funcionaba bien para los valores de corner-shape que son redondos o más convexos que eso (por ejemplo, squircle) y se puede rotar 90 grados para formas más cóncavas que un scoop, este valor predeterminado no funciona para los valores de corner-shape entre -1 y 1, ya que desplazar el borde o la sombra de forma paralela al borde produce una esquina que parece tener un ancho desigual.
Por ejemplo, tomar una esquina bevel y desplazar el borde algunos píxeles hacia ambos lados crea un efecto de "panza", en el que el centro de la esquina se ve más ancho que los lados.
Para tener en cuenta esto, el objetivo es crear un efecto que funcione como un trazo: encuentra la normal de la curva de la esquina al principio y hazla tan larga como el ancho del border o el shadow-spread.
Por suerte, esto solo es necesario para las subelipses (entre bevel y round), ya que las hiperelipses, como squircle, funcionan según lo esperado.
Para encontrar la normal de una curva de subelipse, basta con encontrar la normal de su curva cuadrática equivalente, ya que las subelipses y sus equivalentes de curva cuadrática son similares.
Con el mismo medio ángulo calculado antes, puedes encontrar una curva cuadrática que tenga el mismo punto medio, derivar su punto de control cuadrático y, a partir de ahí, calcular la normal es sencillo.
La normal continúa con la misma longitud que border-width o shadow-spread y, luego, recorta la curva resultante con los bordes (borde interno para el borde, borde externo para la sombra) para crear una ruta continua.
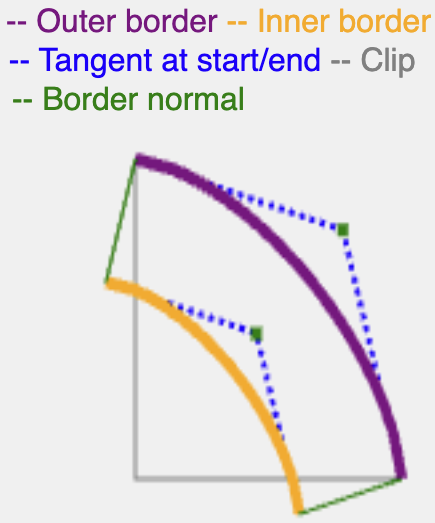
Existen formas más precisas desde el punto de vista matemático para calcular una tangente para un superellipse, pero este método es eficiente y produce resultados adecuados para renderizar bordes y sombras.
Uniones de color
Una parte interesante de la pintura que ocurre en los navegadores no se especifica en CSS. Renderiza bordes que tienen colores o estilos no uniformes. Por ejemplo, donde tu elemento tiene un borde superior sólido de color verde y un borde derecho punteado de color amarillo. En estos casos, la inglete es una línea de incisión que va desde la esquina pertinente del borde hasta la esquina pertinente del borde del padding. Crea el límite entre los bordes adyacentes.Si bien no se especifica, la renderización es algo coherente entre los navegadores.
La forma en que se implementa en Blink (y en otros navegadores) es la siguiente. El borde que se está por pintar se recorta de forma aproximada como un polígono que se cruza en la inglete, calculado de tal manera que incluiría el borde pertinente, pero no ninguno de los otros bordes. Esto evita el sangrado, que consiste en pintar uno de los otros bordes con el color y el estilo incorrectos.
Hasta ahora, este polígono era relativamente simple de calcular, ya que, con esquinas redondeadas regulares, las áreas de las esquinas nunca se pueden superponer. Sin embargo, esto cambia con las hipoelipses y, específicamente, con las superelipses cóncavas (valores de superellipse negativos). Estos pueden crear formas bastante interesantes que hacen que los polígonos de intersección ingenuos sean muy propensos a superposiciones y "sangrado".
Considera el siguiente código CSS:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
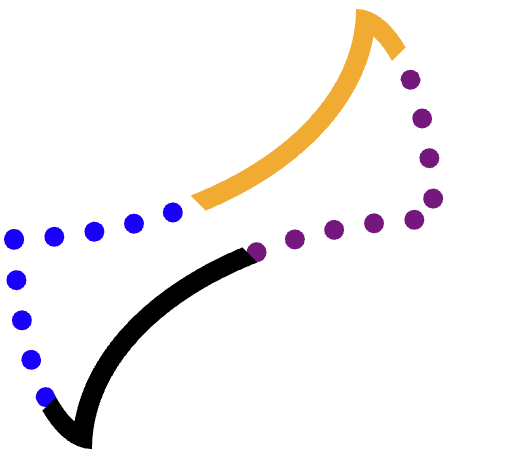
Queremos recortar cada borde (naranja, con puntos morados, negro, con puntos azules) por separado y, luego, dibujar la ruta.
Para lograr esto sin superponer ninguna de las otras tres esquinas, es necesario realizar un recorte cuidadoso.
Por ejemplo, considera el borde naranja (superior).
Es difícil encontrar un polígono exacto que incluya todo ese borde y no se extienda hacia los bordes morados, amarillos o incluso negros. Otras formas son más difíciles.
Este proceso incluye tres clips.
El primer clip incluye todo el borde, con la esquina completa (sin inglete). Por ejemplo:

Consta de dos esquinas (una scoop y una redonda), con un borde mínimo entre ellas, conectadas en los extremos.
Comenzar con esta forma elimina las superposiciones con el borde opuesto, y ahora solo las dos uniones en inglete siguen siendo un problema.
Para lograrlo, se recorta, desde esta esquina, un polígono que pasa entre las esquinas del borde y del padding, y se detiene en el momento en que está a punto de intersecarse con el borde:
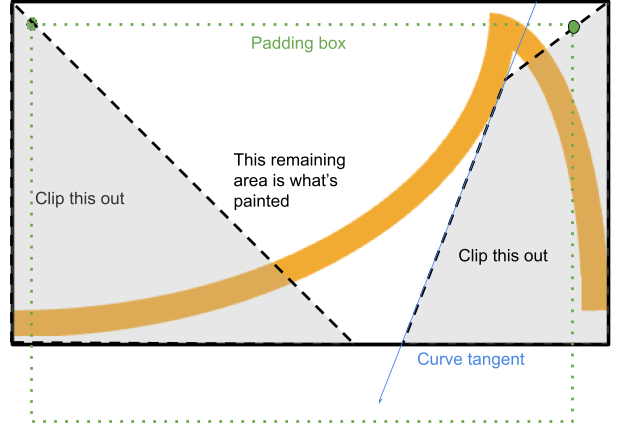
El sistema encuentra el punto en el que una línea desde el borde del límite hasta el borde del padding se cruza con la tangente de la curva desde el punto de partida pertinente (si la curva es cóncava).
Si ese punto está dentro del área renderizada, el proceso se detiene allí y continúa a lo largo de esa tangente hasta que se vuelve a encontrar con el cuadro delimitador, lo que completa un cuadrilátero.
De lo contrario, se puede recortar un triángulo simple.
Resumen
La plataforma web proporciona a los diseñadores y desarrolladores web una gran capacidad de expresión. A veces, una propiedad de CSS que toma un solo valor numérico oculta una complejidad significativa para que se renderice de forma precisa y coherente.
La función corner-shape tenía una complejidad sorprendente. El objetivo de esta documentación es ayudar a los futuros desarrolladores que trabajen en esta función, ya sea en Blink, otros navegadores o la especificación.

