מקרים מיוחדים בהטמעה של צורת פינה ב-CSS ב-Blink

Noam Rosenthal

תאריך פרסום: 19 בפברואר 2026

אחת מתכונות ה-CSS ש-Chrome השיקה בשנת 2025 הייתה corner-shape. כך אפשר להגדיר את הצורה של פינה עם border-radius באמצעות מילות מפתח כמו bevel ו-scoop. אפשר גם להשתמש בפונקציה superellipse שמקבלת ערך בין -Infinity ל-Infinity.

במאמר המקיף של עמית שיין ב-Frontend Masters יש סקירה מצוינת של התכונה והסבר על אופן הפעולה שלה.

במהלך ההטמעה של התכונה הזו בתחילת 2025, נתקלתי בכמה אתגרים מעניינים ברמות מורכבות שונות. למדתי הרבה על סופר-אליפסות, על ציור גבולות ב-Blink ועל שימוש במתמטיקה וקטורית לגרפיקה דו-ממדית.

במסמך הזה אני משתף חלק מהדברים שלמדתי, שאולי יעניינו גם אחרים.

סימטריה של צורות קמורות וקעורות

בדרך כלל, הערכים של superellipse (k) הם בין 0 ל-Infinity, כאשר ערכים בין 0 ל-1 הם קעורים והשאר הם קמורים (1 הוא bevel). ערכי superellipse במפרט CSS הם בין -Infinity ל-Infinity, ומייצגים 2k. כך נוצרת סימטריה, כי כל ערך חיובי נראה כמו תמונת המראה של הערך השלילי המקביל.

עם זאת, כברירת מחדל, הנוסחה superellipse לא פועלת כך.

הנוסחה של superellipse היא: xk + yk = 1. הנוסחה ההפוכה, x1/k + y1/k = 1, לא יוצרת עקומה סימטרית מבחינה חזותית.

לדוגמה, עם k של 2:

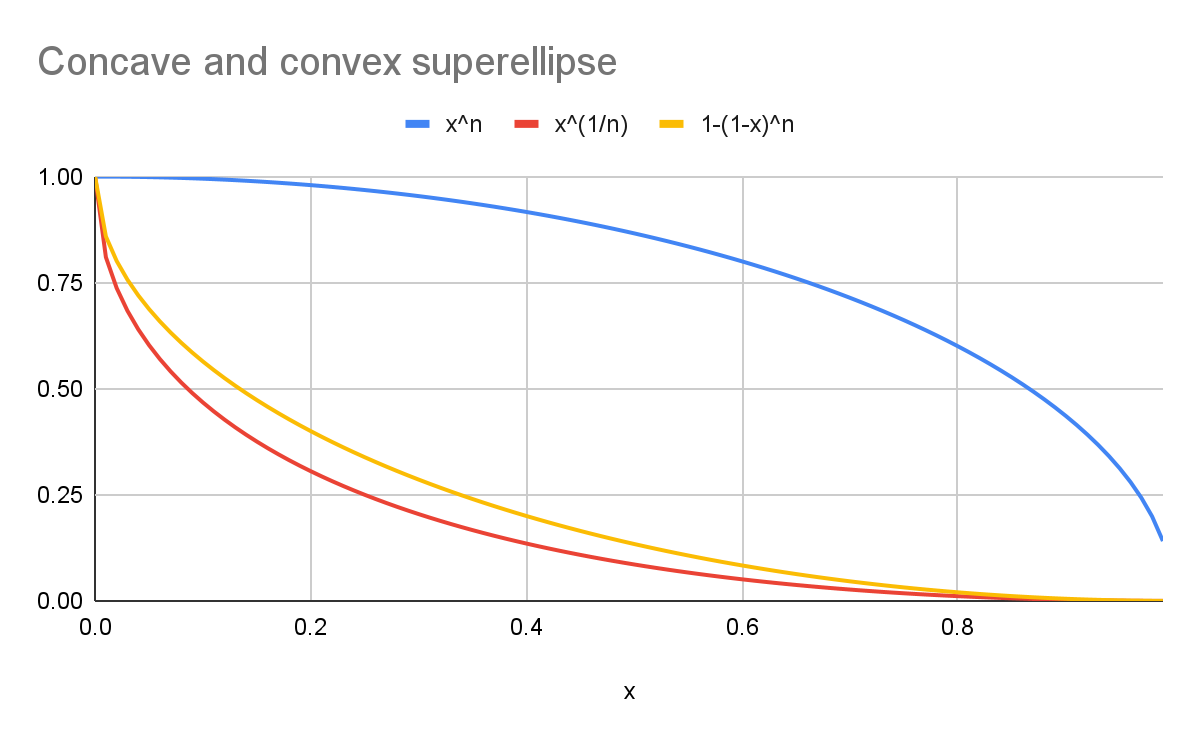
• הקו הכחול מייצג סיבוב superellipse (y=xn).
• העקומה האדומה מייצגת scoop superellipse עם הנוסחה הקנונית (y=x1/n).
• העקומה הצהובה מייצגת עקומה שסימטרית מבחינה ויזואלית לעקומה הכחולה (y=1-(1-x)n).

כפי שאפשר לראות בתרשים, הצורות לא זהות.

לא אכנס לפרטים המתמטיים, אבל זה קשור לנורמות כפולות ולאופן שבו אנחנו תופסים עקמומיות.

מבחינת המפרט וההטמעה, אנחנו מייצגים כאן משהו ויזואלי, ולכן אנחנו משתמשים במקבילות הסימטריות כשמחשבים צורות קעורות. שאר החישובים מתבצעים על צורות קמורות (k>=1 או ערכים חיוביים של סופר-אליפסה).

נוסחה של טופס סגור

האתגר הבא הוא לייצג את העקומה, או את ההיקף של superellipse, בצורה סגורה, כלומר בנוסחה שמורכבת מפעולות חשבון פשוטות. הפעולה הזו חיונית לביצועים, כי היא מאפשרת למערכת להעביר את superellipse העיבוד למנוע הגרפי.

מנועי גרפיקה כמו Skia מכירים עקומות בזייה, ולכן ייצוג של superellipse באמצעות מספר קטן של עקומות בזייה שמבצעות קירוב של ההיקף שלו משפר את הביצועים של עיבוד עקומת superellipse.

למזלנו, באמצעות רגרסיה סמלית, אנחנו יכולים למצוא נוסחה שמייצגת חצי פינה קמורה כעקומת בזייה קובייתית אחת.

לעקומת בזייה מעוקבת יש ארבע נקודות:

• הנקודה הראשונה היא (0, 1).
• הנקודה האחרונה היא חצי הפינה של הסופר-אליפסה: 0.51/k,0.51/k.
• נקודת הבקרה הראשונה נמתחת פנימה באותה רמה של נקודת ההתחלה: (a, 1).
• נקודת הבקרה השנייה היא אלכסונית למחצית הפינה: (0.51/k - b,0.51/k + b).

הערך של חצי הפינה שבו השתמשנו כאן הוא במקרה קואורדינטה חשובה מאוד שנשתמש בה לחישובים אחרים בהמשך.

כאשר a ו-b מחושבים מ-k באמצעות רגרסיה סימבולית.

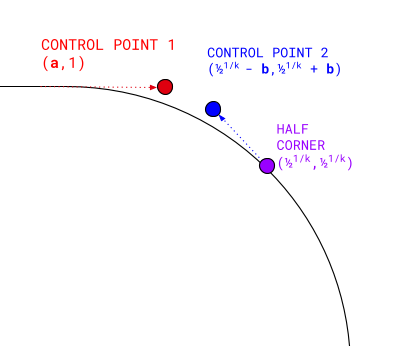
חישוב ארבע הנקודות האלה ועיבוד של עקומת בזייה מעוקבת ביניהן מספק צורה סגורה של חצי פינה קמורה עם k נתון. אחר כך אפשר לסובב את התוצאות כדי למלא את שאר הפינה, להחיל אותן על פינות אחרות ולהפוך אותן כדי להציג את הגרסאות הקעורות.

בלי להיכנס יותר מדי לפרטים המתמטיים, הנוסחה לחישוב a ו-b היא:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

גבולות וצללים

בנוסף לחישוב הנתיב של היקף הפינה, המערכת מחשבת גם איך היא נראית כשהיא מוזזת פנימה (גבול או שקע box-shadow) או החוצה (outline או box-shadow רגיל). בספריות גרפיות רגילות, הפעולה הזו מתבצעת באמצעות משיכת קו.

עם זאת, למסגרות ולצללים ב-CSS יש מאפייני רינדור ששונים ממאפייני הרינדור של קו מתאר:

• הגבולות לא אחידים.
• לדוגמה, הגבול העליון יכול להיות 10 פיקסלים והגבול הימני 5 פיקסלים, והפינה תהיה אינטרפולציה ביניהם.
• בנוסף, הן מתרחבות פנימה ולא לצדדים.
• הצלליות והמתארים לא מוצגים בדיוק כמו קו.
• במקום זאת, הן מתכווננות כך שהפינות ייראו חדות.

בדרך כלל, עיבוד הגבול והצל עובד טוב עם ערכים של corner-shape שהם מעוגלים או קמורים יותר (לדוגמה, squircle), ואפשר לסובב אותם ב-90 מעלות לצורות שהן קעורות יותר מ-scoop. עם זאת, הגדרת ברירת המחדל הזו לא עובדת עם ערכים של corner-shape בין -1 ל-1, כי הזזת הגבול או הצל במקביל לקצה יוצרת פינה שנראית כאילו הרוחב שלה לא אחיד.

לדוגמה, אם לוקחים bevel פינה ומסיטים את הגבול בכמה פיקסלים לשני הצדדים, נוצר אפקט של 'בטן', שבו החלק האמצעי של הפינה נראה רחב יותר מהצדדים.

כדי להתמודד עם זה, המטרה היא ליצור אפקט שפועל כמו קו – מוצאים את הנורמל של עקומת הפינה בהתחלה, ויוצרים אותו באורך של הרוחב של border או shadow-spread.

למזלנו, זה נחוץ רק עבור תת-אליפסות (בין bevel לבין round), כי היפר-אליפסות כמו squircle פועלות כמו שצריך.

כדי למצוא את הנורמל של עקומת תת-אליפסה, מספיק למצוא את הנורמל של עקומת המקבילה הריבועית שלה, כי תת-אליפסות והמקבילות הריבועיות שלהן קרובות זו לזו.

באמצעות אותה נקודת אמצע שחושבה קודם, אפשר למצוא עקומה ריבועית עם אותה נקודת אמצע, לגזור את נקודת הבקרה הריבועית שלה, ומכאן החישוב של הנורמל הוא פשוט.

הקו ממשיך כרגיל באורך זהה ל-border-width או ל-shadow-spread, ואז הוא נחתך בקצוות (הקצה הפנימי לגבול, הקצה החיצוני לצל) כדי ליצור נתיב רציף.

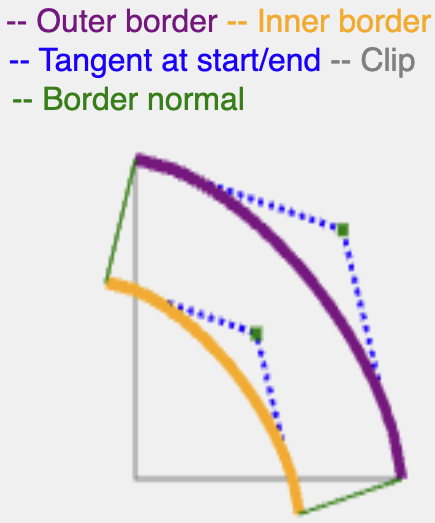
יש דרכים מדויקות יותר מבחינה מתמטית לחשב טנגנס לזווית superellipse, אבל השיטה הזו יעילה ומניבה תוצאות מספיקות לעיבוד גבולות וצללים.

הצבעים מתמזגים

מעניין לציין שחלק מהפעולות שמתבצעות בדפדפנים כשמציירים תמונות לא מוגדרות ב-CSS. הוא מעבד גבולות עם צבעים או סגנונות לא אחידים. לדוגמה, אם לרכיב יש גבול עליון ירוק מלא וגבול ימני צהוב מקווקו. במקרים כאלה, החיתוך הוא קו חיתוך שעובר בין הפינה הרלוונטית של קצה הגבול לבין הפינה הרלוונטית של קצה הריווח הפנימי. הוא יוצר את הגבול בין הקצוות הסמוכים.למרות שלא צוין, העיבוד די עקבי בין הדפדפנים.

ההטמעה של התכונה הזו ב-Blink (ובדפדפנים אחרים) מתבצעת באופן הבא. הקצה שעומד להיצבע נחתך בצורה גסה כמו פוליגון שחוצה את המפגש, ומחושב כך שיכלול את הקצה הרלוונטי אבל לא את הקצוות האחרים. כך נמנע טשטוש, שגורם לצביעת אחד מהקצוות האחרים בסגנון ובצבע שגויים.

עד עכשיו, החישוב של המצולע היה פשוט יחסית, כי בפינות מעוגלות רגילות, האזורים של הפינות אף פעם לא יכולים לחפוף. עם זאת, המצב משתנה כשמדובר בהיפו-אליפסות, ובמיוחד בסופר-אליפסות קעורות (ערכי superellipse שליליים). הן יכולות ליצור צורות מעניינות למדי שגורמות למצולעים наивные intersection להיות מועדים מאוד לחפיפות ול "זליגה".

נניח שיש לכם את ה-CSS הבא:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}

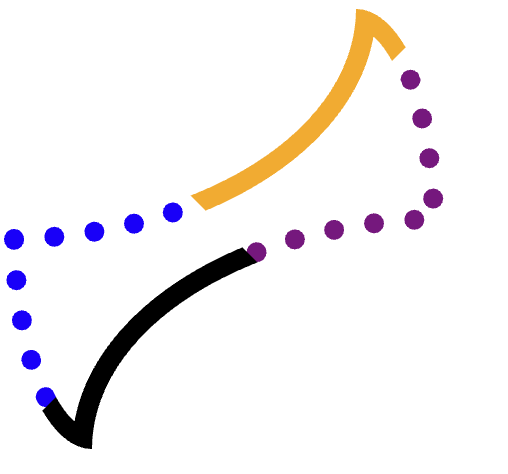
אנחנו רוצים לחתוך כל קצה (כתום, סגול עם נקודות, שחור, כחול עם נקודות) בנפרד, ואז לצייר את הנתיב.

כדי לעשות את זה בלי לחפוף לאף אחת משלוש הפינות האחרות, צריך לחתוך בזהירות.

לדוגמה, נסתכל על הקצה הכתום (העליון).

קשה למצוא מצולע מדויק שכולל את כל הקצה הזה ולא חורג אל הקצוות הסגולים, הצהובים או אפילו השחורים. צורות אחרות מאתגרות יותר.

התהליך הזה כולל שלושה קליפים.

הקליפ הראשון כולל את כל הקצה, עם הפינה המלאה (ללא חיתוך בזווית). לדוגמה:

הוא מורכב משתי פינות (אחת scoop ואחת מעוגלת), עם קצה מינימלי ביניהן, שמחוברות בקצוות.

התחלה מהצורה הזו מבטלת חפיפות עם הקצה הנגדי, ועכשיו רק שני החיתוכים האלכסוניים נשארים בעיה.

הפעולה הזו מתבצעת על ידי חיתוך של מצולע מהפינה הזו, שעובר בין הפינות של שולי הגבול והריווח, ומסתיים ברגע שהוא עומד להצטלב עם הקצה:

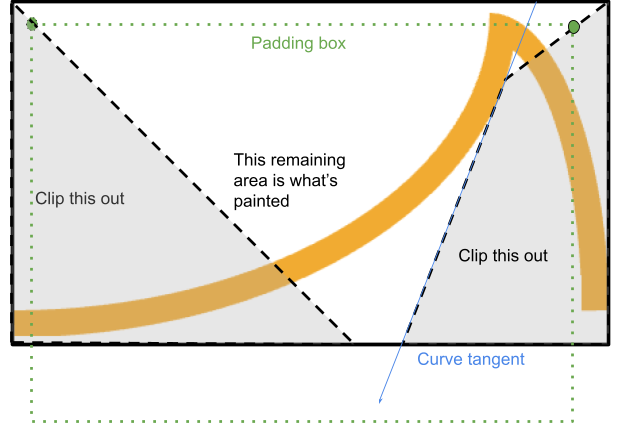
המערכת מוצאת את הנקודה שבה קו מקצה הגבול לקצה הריווח מצטלב עם המשיק של העקומה מנקודת ההתחלה הרלוונטית (אם העקומה קעורה).

אם הנקודה הזו נמצאת בתוך האזור המעובד, התהליך נעצר שם וממשיך לאורך המשיק עד שהוא פוגש שוב את תיבת הגבול, וכך נוצר מרובע.

אחרת, אפשר לחתוך משולש פשוט.

סיכום

פלטפורמת האינטרנט מספקת למעצבי אתרים ולמפתחים יכולות ביטוי משמעותיות. לפעמים מאחורי נכס CSS שמקבל ערך מספרי יחיד מסתתרת מורכבות משמעותית, כדי שהעיבוד שלו יהיה מדויק ועקבי.

התכונה corner-shape הייתה מורכבת באופן מפתיע. מטרת מסמכי התיעוד האלה היא לעזור למפתחים עתידיים שיעבדו על התכונה הזו ב-Blink, בדפדפנים אחרים או במפרט.