Pubblicato: 19 febbraio 2026
Una delle funzionalità CSS rilasciate da Chrome nel 2025 è
corner-shape.
In questo modo puoi definire la forma di un angolo che ha un border-radius utilizzando
parole chiave come bevel e scoop. Puoi anche utilizzare una funzione superellipse
che riceve un valore compreso tra -Infinity e Infinity.
Consulta l'articolo dettagliato di Amit Sheen su Frontend Masters per una panoramica completa della funzionalità e del suo funzionamento.
Quando ho implementato questa funzionalità all'inizio del 2025, ho riscontrato alcune sfide interessanti di varia complessità. Ho imparato molto su superellissi, pittura dei bordi in Blink e utilizzo della matematica vettoriale per la grafica 2D.
Questo documento condivide alcune delle cose che ho imparato, che potrebbero essere interessanti anche per altri.
Simmetria di forme convesse e concave
Mentre i valori di superellipse (k) vanno tradizionalmente da 0 a Infinity, dove
i valori compresi tra 0 e 1 sono concavi e gli altri sono convessi (1 è bevel),
i valori di superellipse nella specifica CSS vanno da -Infinity a Infinity e
rappresentano 2k. In questo modo si crea una simmetria, in quanto qualsiasi valore positivo appare come
l'immagine speculare della sua controparte negativa.
Tuttavia, per impostazione predefinita, la formula superellipse non funziona in questo modo.
La formula per superellipse è: xk + yk = 1. La formula inversa, x1/k + y1/k = 1, non produce una curva visivamente simmetrica.
Ad esempio, con un k di 2:
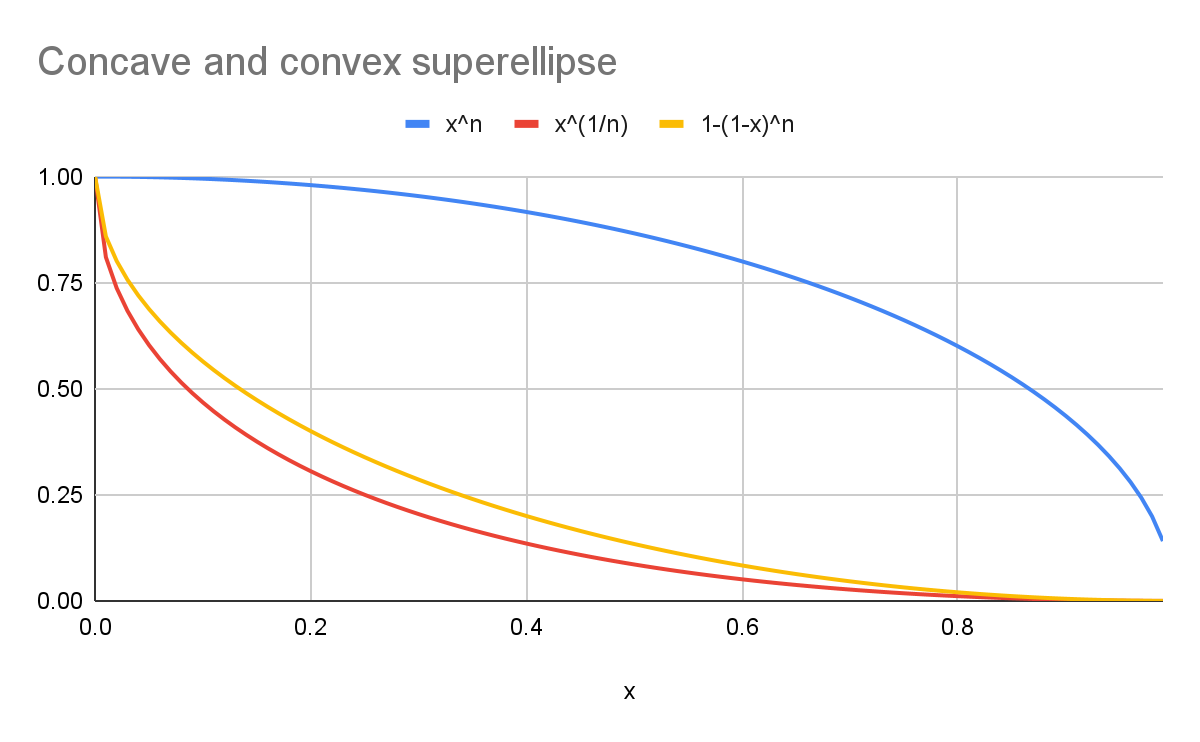
- La curva blu rappresenta un round
superellipse(y=xn). - La curva rossa rappresenta una
scoopsuperellipsecon la formula canonica (y=x1/n). - La curva gialla rappresenta una curva visivamente simmetrica a quella blu (
y=1-(1-x)n).
Come mostra il grafico, le forme non sono uguali.
Non approfondirò l'aspetto matematico, ma ha a che fare con le norme duali e con il modo in cui percepiamo la curvatura.
In termini di specifica e implementazione, qui rappresentiamo qualcosa
di visivo, quindi utilizziamo gli equivalenti simmetrici per calcolare le forme
concave. Il resto dei calcoli viene eseguito su forme convesse (k>=1 o valori di superellisse positivi).
Formula in forma chiusa
La prossima sfida è rappresentare la curva, o il perimetro di superellipse, in forma chiusa, una formula composta da semplici operazioni aritmetiche.
Questo è essenziale per le prestazioni, in quanto consente al sistema di trasferire il rendering superellipse al motore grafico.
I motori grafici come Skia conoscono le curve di Bézier, quindi rappresentare un superellipse con un piccolo numero di curve di Bézier che
approssimano il suo perimetro rende il rendering di una curva superellipse più efficiente.
Fortunatamente, utilizzando la regressione simbolica, possiamo trovare una formula che rappresenti metà di un angolo convesso come una singola curva di Bézier cubica.
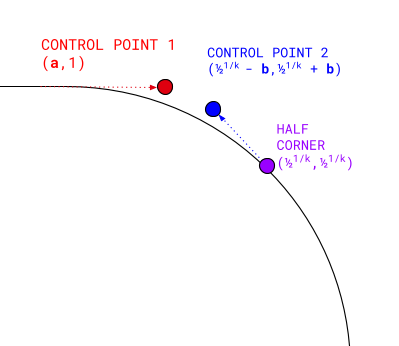
Una curva di Bézier cubica ha quattro punti:
- Il primo punto è (
0, 1). - L'ultimo punto è l'angolo effettivo della superellisse:
0.51/k,0.51/k. - Il primo punto di controllo si estende allo stesso livello del punto
di partenza: (
a, 1). - Il secondo punto di controllo è in diagonale rispetto a metà angolo:
(0.51/k - b,0.51/k + b).
Il valore del mezzo angolo utilizzato qui è una coordinata molto importante che utilizzeremo per altri calcoli in futuro.
dove a e b vengono calcolati da k utilizzando la regressione simbolica.
Il calcolo di questi quattro punti e il rendering di una curva di Bézier cubica tra loro fornisce un angolo convesso chiuso con un k specificato. Possiamo quindi ruotare i risultati per riempire il resto dell'angolo, applicarli ad altri angoli e capovolgerli per
renderizzare gli equivalenti concavi.
Senza entrare troppo nei dettagli matematici, la formula per calcolare a
e b è la seguente:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Bordi e ombre
Oltre a calcolare il percorso del perimetro dell'angolo, il sistema calcola anche il suo aspetto quando viene spostato verso l'interno (un bordo o un rientro box-shadow) o
verso l'esterno (un outline o un box-shadow normale). Nelle librerie grafiche convenzionali, questa operazione viene eseguita tramite il tratto.
Tuttavia, i bordi e le ombre in CSS hanno caratteristiche di rendering diverse dalla traccia:
- I bordi non sono uniformi.
- Ad esempio, il bordo superiore può essere di 10 pixel e il bordo destro di 5 pixel, con l'angolo che interpola tra i due.
- Inoltre, si piegano verso l'interno anziché su entrambi i lati.
- Ombre e contorni non vengono visualizzati esattamente come un tratto.
- ma vengono regolate in modo che gli angoli appaiano nitidi.
Sebbene il percorso di rendering di bordi e ombreggiature funzioni bene per i valori di corner-shape arrotondati o più convessi (ad esempio, squircle) e possa essere ruotato di 90 gradi per le forme più concave di un scoop, questo valore predefinito non funziona per i valori di corner-shape compresi tra -1 e 1, poiché l'offset del bordo o dell'ombreggiatura parallelo al bordo produce un angolo che sembra avere una larghezza irregolare.
Ad esempio, prendendo un angolo bevel e spostando il bordo di alcuni pixel su entrambi i lati si crea un effetto "pancia", in cui la parte centrale dell'angolo appare più ampia dei lati.
Per tenerne conto, l'obiettivo è creare un effetto simile a un tratto: trova
la normale della curva dell'angolo all'inizio e rendila lunga quanto la larghezza
di border o shadow-spread.
Fortunatamente, questo è necessario solo per le sottoellissi (tra bevel e rotondo), poiché le iperellissi come squircle funzionano come previsto.
Per trovare la normale di una curva subellittica, è sufficiente trovare la normale della sua controparte della curva quadratica, poiché le subellissi e le loro curve quadratiche equivalenti sono vicine tra loro.
Utilizzando lo stesso mezzo angolo calcolato in precedenza, puoi trovare una curva quadratica che ha lo stesso punto medio, derivare il suo punto di controllo quadratico e da lì calcolare la normale è semplice.
La normale continua con la stessa lunghezza di border-width o shadow-spread, quindi taglia la curva risultante con i bordi (bordo interno per il bordo, bordo esterno per l'ombra) per creare un percorso continuo.
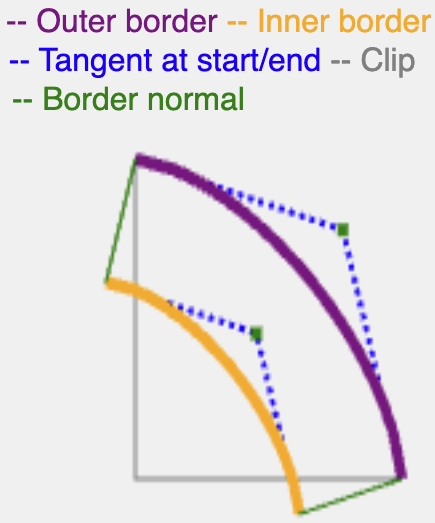
Esistono modi più precisi dal punto di vista matematico per calcolare una tangente per un superellipse, ma questo metodo è efficiente e produce risultati adeguati per il rendering di bordi e ombre.
Unioni di colori
Un aspetto interessante della pittura che si verifica nei browser non è specificato in CSS. Esegue il rendering dei bordi con colori o stili non uniformi. Ad esempio, se l'elemento ha un bordo superiore verde pieno e un bordo destro giallo punteggiato. In questi casi, la smussatura è una linea di incisione che va da l'angolo pertinente del bordo del bordo all'angolo pertinente del bordo del padding. Crea il confine tra i bordi adiacenti.Anche se non specificato, il rendering è in qualche modo coerente tra i browser.
Il modo in cui viene implementato in Blink (e in altri browser) è il seguente. Il bordo che sta per essere dipinto viene ritagliato grossolanamente come un poligono che attraversa la mitra, calcolato in modo da includere il bordo pertinente ma non gli altri bordi. In questo modo si evita lo sanguinamento, ovvero la pittura di uno degli altri bordi con lo stile e il colore errati.
Questo poligono è stato finora relativamente semplice da calcolare, perché con gli angoli arrotondati regolari le aree degli angoli non possono mai sovrapporsi. Tuttavia, questo cambia con le ipoellissi e in particolare con le superellissi concave (valori negativi di superellipse). Questi possono creare forme piuttosto interessanti che rendono i
poligoni di intersezione ingenui molto inclini a sovrapposizioni e "sanguinamenti".
Considera il seguente CSS:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
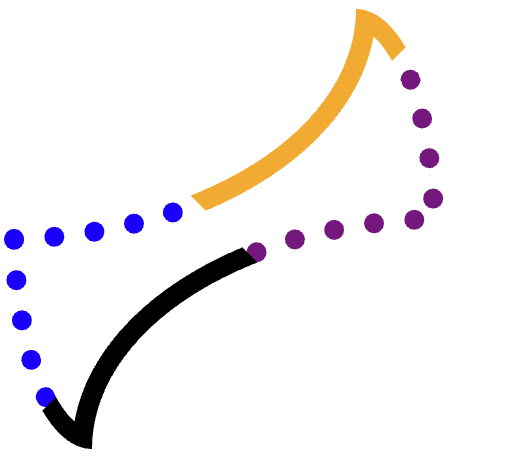
Vogliamo ritagliare separatamente ogni bordo (arancione, viola tratteggiato, nero, blu tratteggiato) e poi disegnare il percorso.
Per ottenere questo risultato senza sovrapporre nessuno degli altri tre angoli, è necessario un ritaglio accurato.
Ad esempio, considera il bordo arancione (superiore).
È difficile trovare un poligono esatto che includa l'intero bordo e non si estenda ai bordi viola, gialli o persino neri. Altre forme sono più difficili.
Questa procedura prevede tre clip.
Il primo clip include l'intero bordo, con l'angolo completo (senza smusso). Ad esempio:

È composto da due angoli (uno scoop e uno arrotondato), con un bordo minimo tra loro, collegati alle estremità.
Partendo da questa forma si eliminano le sovrapposizioni con il bordo opposto e ora rimangono un problema solo i due angoli.
Ciò si ottiene ritagliando da questo angolo un poligono che passa tra gli angoli del bordo e del padding e si ferma nel momento in cui sta per intersecarsi con il bordo:
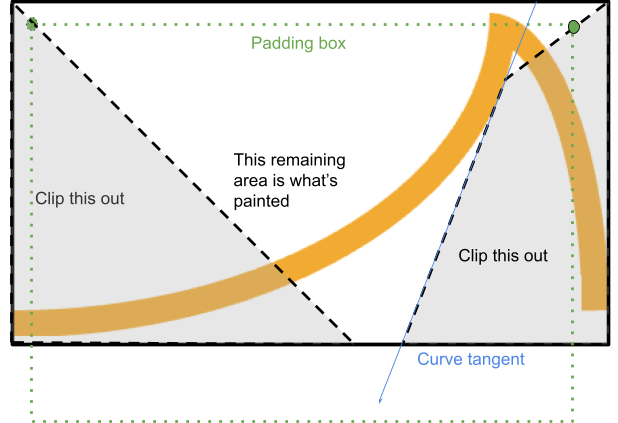
Il sistema trova il punto in cui una linea dal bordo al bordo del padding si interseca con la tangente della curva dal punto di partenza pertinente (se la curva è concava).
Se questo punto si trova all'interno dell'area di rendering, il processo si arresta e continua lungo la tangente fino a quando non incontra di nuovo il riquadro di selezione, completando un quadrilatero.
In caso contrario, è possibile ritagliare un semplice triangolo.
Riepilogo
La piattaforma web offre a web designer e sviluppatori un'espressività significativa. A volte, una proprietà CSS che accetta un singolo valore numerico nasconde una complessità significativa sotto il cofano per renderla in modo accurato e coerente.
La funzionalità corner-shape si è rivelata sorprendentemente complessa. Questa documentazione ha lo scopo di aiutare gli sviluppatori futuri che lavorano su questa funzionalità in Blink, in altri browser o nella specifica.

